In the last class, we defined the conditional probability of $A$ given $B$ as $\Pr(A \mid B) = \frac{\Pr(A \cap B)}{\Pr(B)}$ for non-empty $B$. By rearranging the equation slightly, we get $\Pr(A \cap B) = \Pr(A \mid B) \cdot \Pr(B)$, which allows us to make the following observation, named after the Presbyterian minister and statistician Thomas Bayes.
Theorem 19.1 (Bayes' Theorem). If $A$ and $B$ are events with $\Pr(A), \Pr(B) \gt 0$, then $$\Pr(A \mid B) = \frac{\Pr(B \mid A) \cdot \Pr(A)}{\Pr(B)}$$
Proof. We know that $$\Pr(A \mid B) \Pr(B) = \Pr(A \cap B) = \Pr(B \mid A) \Pr(A)$$ Dividing all the terms by $\Pr(B)$ get us the desired result. $\tag*{$\Box$}$
Definition 19.2. A partition of $\Omega$ is a family of pairwise disjoint events $H_1, \dots, H_m$ covering $\Omega$. That is, $\bigcup_{i=1}^m H_i = \Omega$ and $H_i \cap H_j = \emptyset$ for all $i \neq j$.
Theorem 19.3 (Law of Total Probability). Given a partition $H_1, \dots, H_m$ of $\Omega$ and an event $A$, $$\Pr(A) = \sum_{i=1}^m \Pr(A \cap H_i).$$
Proof. Since we have a partition $H_1, \dots, H_m$, we have $A = A \cap \Omega = A \cap \bigcup_{i = 1}^m H_i$. Then, \begin{align*} \Pr(A) &= \Pr\left( A \cap \bigcup_{i=1}^m H_i \right) \\ &= \Pr \left( \bigcup_{i=1}^m (A \cap H_i) \right) \\ &= \sum_{i=1}^m \Pr(A \cap H_i) &\text{since $H_i$ are pairwise disjoint} \\ \end{align*} $\tag*{$\Box$}$ This can be rewritten as $$\Pr(A) = \sum_{i=1}^m \Pr(A \mid H_i) \cdot \Pr(H_i).$$
The Law of Total Probability generalizes the idea that if I know $\Pr(A \cap B)$ and I know $\Pr(A \cap \overline B)$, then that just gives me $\Pr(A)$ when I put them together. The Law of Total Probability will be particularly useful for computing the probabilities of events when applying Bayes' Theorem.
Example 19.4. Consider a medical device used to test people for a kind of cancer. This kind of cancer occurs in 1% of the population, that is, $\Pr(C) = 0.01$. The test is relatively accurate, the chance that somebody with cancer tests postive $\Pr(P \mid C)$ is $0.9$ (called the true positive rate or sensitivity) and the probability that somebody without cancer tests positive $\Pr(P \mid \neg C)$ is $0.09$ (the false positive rate). If a random person tests positive, what is the probability they have cancer?
We want to know $\Pr(C \mid P)$. Using Bayes' Theorem, we can write this as $$\Pr(C \mid P) = \frac{\Pr(P \mid C)\Pr(C)}{\Pr(P)} = \frac{0.9 \cdot 0.01}{\Pr(P)}$$
By the law of total probability, $$\Pr(P) = \Pr(P \mid C)\Pr(C) + \Pr(P \mid \neg C)\Pr(\neg C) = 0.9 \cdot 0.01 + 0.09 \cdot 0.99$$ Hence $$\Pr(C \mid P) = \frac{0.9 \cdot 0.01}{0.9 \cdot 0.01 + 0.09 \cdot 0.99} \approx \frac{0.009}{0.009 + 0.09} = \frac{1}{11}$$ $\tag*{$\Box$}$
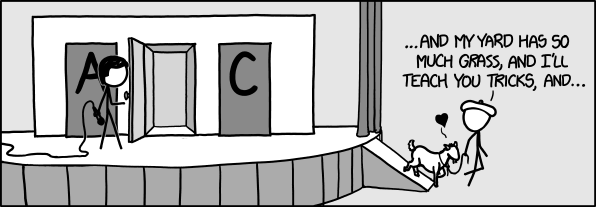
Example (Monty Hall) 19.5. The Monty Hall problem is a classic example of conditional probability and independence and it initially stumpe a remarkable number of serious mathematicians. The story is loosely based on the game show Let's Make a Deal, whose host was a guy by the name of Monty Hall.
Suppose there are three doors and there is a prize behind each door. Behind one of the doors is a car and behind the other two are goats. So you pick a door. The host will then choose a door to open that reveals a goat. You are then given the option to either stick with your original choice or to change your choice to the remaining closed door. Should you switch?
There two possible intuitions for this problem. The first is that the goat was equally likely to be behind any one of the three doors. Now that one door has been removed from the equation, the goat is equally likely to be behind each door, for a probability of $\frac{1}{2}$.
The other intuition is that we had an initial probability of $\frac{2}{3}$ of getting a goat. Given that Monty will always reveal the other goat, if my initial choice was wrong, I would win by switching. Hence the probability of winning if I switch is $\frac{2}{3}$.
Since there are two opposing intuitions here, lets just do the math. For simplicity, let us assume you chose door number 1. We'll write $C_i$ for "the car is behind door i" and $M_i$ for "Monty picks door i". Initially the car is equally likely to be behind door 1, 2 or 3. If it's behind door 2 or 3, Monty's choice is determined, so $\Pr(M_3 \mid C_2) = \Pr(M_2 \mid C_3) = 1$. By contrast, $\Pr(M_2 \mid C_1) = \Pr(M_3 \mid C_1) = \frac{1}{2}$, assuming that Monty is equally likely to pick from each door. (Note that this is an implicit assumption not stated in the puzzle. If Monty always picks door 2 when available, these odds change, which makes for a nice exercise.) Applying Bayes' Theorem to the case where Monty picks door number 2: $$\Pr(C_1 \mid M_2) = \frac{\Pr(M_2 \cap C_1)\Pr(C_1)}{\Pr(M_2)} = \frac{1/2 \cdot 1/3}{1/2} = \frac{1}{3}$$ whereas $$\Pr(C_3 \mid M_2) = \frac{\Pr(M_2 \cap C_3)\Pr(C_3)}{\Pr(M_2)} = \frac{1 \cdot 1/3}{1/2} = \frac{2}{3}$$ So it indeed makes sense to switch to door 3.
...assuming you want the car.
Definition 19.6. Events $A$ and $B$ are independent if $\Pr(A \cap B) = \Pr(A) \cdot \Pr(B)$.
This directly implies that if $A$ and $B$ are independent, then $\Pr(A \mid B) = \frac{\Pr(A) \cdot \Pr(B)}{\Pr(B)} = \Pr(A)$, which should fit our intuitions about conditional probability.
Example 19.7. Consider a roll of a two six-sided dice and the events
Clearly, all the $F_i$s and $S_j$ are independent: The second roll doesn't depend on the outcome of the first, or vice-versa. Mathematically, for any $i$ and $j$, $$\Pr(F_i \cap S_j) = \frac{1}{36} = \frac{1}{6} \cdot \frac{1}{6} = \Pr(F_i) \cdot \Pr(S_j)$$ Equally clearly, most $T_k$ are correlated with the $F_i$s: You can't get a total of 11 unless the first die comes up $5$ or $6$. The one exception is $T_7$: $\Pr(T_7 \mid F_i) = \frac{1}{6}$ and likewise for $S_i$. However, obviously $T_7$ isn't independent of the combination of $F_i$ and $S_i$s: $\Pr(T_7 \mid (F_4 \cap S_3)) = 1$ whereas $\Pr(T_7 \mid (F_4 \cap S_4)) = 0$. (We tend to write this as $\Pr(T_7 \mid F_4, S_4) = 0$.) This leads to want to distinguish between the independence of two events in isolation versus a larger group of events.
Definition 19.8. Events $A_1, A_2, \dots, A_k$ are pairwise independent if for all $i \neq j$, $A_i$ and $A_j$ are independent. The events are mutually independent if for every $I \subseteq \{1, \dots, k\}$, $$\Pr \left( \bigcap_{i \in I} A_i \right) = \prod_{i \in I} \Pr(A_i).$$
Definition 19.9. We say events $A$ and $B$ are positively correlated if $\Pr(A \cap B) \gt \Pr(A) \cdot \Pr(B)$ and they are negatively correlated if $\Pr(A \cap B) \lt \Pr(A) \cdot \Pr(B)$.
Example 19.10. Consider a roll of a six-sided die and the events
Are these events independent? If not, how are they related? First, our sample space is $\Omega = \{1,2,3,4,5,6\}$, so our events are going to be $A = \{1,3,5\}$ and $B = \{2,3,5\}$. Then $\Pr(A) = \frac 3 6 = \frac 1 2$ and $\Pr(B) = \frac 3 6 = \frac 1 2$. We want to consider the probability of the intersection of our events. This gives us $$\Pr(A \cap B) = \Pr(\{1,3,5\} \cap \{2,3,5\}) = \Pr(\{3,5\}) = \frac 2 6 = \frac 1 3.$$ But $\Pr(A) \cdot \Pr(B) = \frac 1 2 \cdot \frac 1 2 = \frac 1 4$, which is not $\frac 1 3$, so $A$ and $B$ are not independent. Furthermore, we have $$\Pr(A \cap B) = \frac 1 3 \gt \frac 1 4 = \Pr(A) \cdot \Pr(B),$$ so $A$ and $B$ are positively correlated. Of course, this makes sense intuitively, because we know the only even prime number is 2.